深層学習を用いた時系列データにおける異常検知

Tweet

はじめに

カブクで機械学習エンジニアをしている大串正矢です。今回は深層学習を用いた時系列データにおける異常検知について書きます。

背景

深層学習を異常検知に使用するにあたって閾値設定や評価尺度であるROCについての記述が日本語のウェブの資料で見つけられなかったので本ブログで記述することにしました。以前のブログに異常検知の基礎的な内容があるのでその内容を踏まえた上で読んで頂けると理解がしやすいと思います。

異常検知の基礎
時系列データにおける異常検知

深層学習を用いた時系列データにおける異常検知

• 情報圧縮に関するモデル(AutoEncoderなど)
  • 利点: RNNなどに比べ少ないパラメータで学習可能なため高速
  • 欠点: 系列データ特有の過去の値を考慮した予測ができない
• 系列データに関するモデル(RNNなど)
  • 利点: 系列データ特有の過去の値を考慮した予測が可能
  • 欠点: 構造上、GPU上での並列化が難しいため学習に時間がかかる

本記事では系列データに対するモデルを用いて時系列データの変化点検知を行います。近況ではCNNでも系列データを扱えるようになってきていますが今回は扱いません。

時系列データにおける変化点とは

青の線が通常のデータでそのデータの一部が異常を出した場合、赤の線のようになります。この異常が起きた変化点を検出できると異常が発生した時間を把握できます。

深層学習を用いた異常検知手法

系列データに対するモデルでKerasで比較的に実装が簡単なモデルはLSTMとGRUが存在しています。それぞれの利点と欠点を比較してみます。

• LSTM
  • 利点: パラメータが多いため複雑な時系列データを再現可能
  • 欠点: 他のモデルに比べ学習に時間がかかる
• GRU
  • 利点: LSTMに比べパラメータが少ないので学習が早く、時系列を考慮して学習可能
  • 欠点: LSTMに比べ複雑な波形を再現する能力が若干低いが論文上では性能が変わらないとも言われているので実際に両者を使用して検証した方がベター

データについて

今回、使用するデータは前回の記事で使用した温度変化のデータです。

後述する性能評価のために学習データ、閾値設定のための検証データ、テストデータの3つに分けます。

検証のために下記の異常を加えた波形を作成しました。

• スパイク
• 波形変化
• レベルシフト

スパイク波形の例

波形変化の例

レベルシフトの例

LSTM

通常のRNNでは勾配消失と勾配爆発が起こるため長期依存の学習ができない欠点がありました。
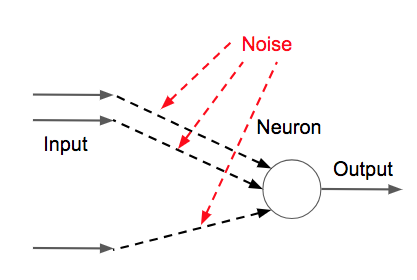
LSTMでは入力と出力と現在の状態の値をリセットするForgetゲートを用意して必要な場合のみ更新することで無駄な入力を入力しない、無駄な出力をしない、入力が急激に変更された場合に現在の状態を更新するなどの処理を実現しています。

下記のようなイメージになります。

隠れ状態を導出する数式は下記になります。

\begin{align}
i &= \sigma(x_tU^i + s_{t-1}W^i) \
\end{align}
\begin{align}
f &= \sigma(x_tU^f + s_{t-1}W^f) \
\end{align}
\begin{align}
o &= \sigma(x_tU^o + s_{t-1}W^o) \
\end{align}
\begin{align}
g &= \tanh(x_tU^g + s_{t-1}W^g) \
\end{align}
\begin{align}
c_t &= c_{t-1} \circ f + g \circ i \
\end{align}
\begin{align}
s_t &= \tanh(c_t) \circ o \
\end{align}

• 時刻: t
• 入力: x
• 入力に対する重み: U
• 状態: s
• 状態に関する重み: W
• 入力ゲート: i
• 忘却ゲート: f
• 出力ゲート: o
• 過去の入力状態のゲート: g
• 内部メモリー（どの程度記憶するか）: c

• 入力、出力、忘却ゲートに関する計算は全てシグモイドによって0から1の値になり、値の通し具合いが極端にならないように調整しています。

• 過去の入力状態のゲートは入力値と過去の状態によって現在の入力を反映させるか過去の状態を反映させるか決定しています。
• 内部メモリーは過去の入力と現在の入力をどのように組み合わせるか決定しています。

GRU

GRUではLSTMとは異なりゲートが二つになり、更新するか、状態をリセットするかになります。

隠れ状態を導出する数式は下記になります。

\begin{align}
z &= \sigma(x_tU^z + s_{t-1}W^z) \
\end{align}
\begin{align}
r &= \sigma(x_tU^r + s_{t-1}W^r) \
\end{align}
\begin{align}
h &= \tanh(x_tU^h + (s_{t-1} \circ r)W^h) \
\end{align}
\begin{align}
s_t &= (1-z) \circ h + z \circ s_{t-1}
\end{align}

• 時刻: t
• 入力: x
• 入力に対する重み: U
• 状態: s
• 状態に関する重み: W
• 更新ゲート: z
• リセットゲート:r

• 過去の状態を記憶する内部メモリーは存在しません。

• 更新ゲートは今の状態のリセットと入力に適用され、リセットゲートは過去の状態に適用されるためリセットの責務はリセットゲートと更新ゲートに分かれています。

LSTM・GRUに関する説明は簡易的なものなので詳しく知りたい方は下記のブログが分かりやすいためので興味がある方はご覧ください

• LSTM・GRU
  • https://qiita.com/t_Signull/items/21b82be280b46f467d1b

コードによる実装

notebook上に全てのコードは載せているので確認したい方は下記をご覧ください

https://github.com/SnowMasaya/time_series_anomaly_detect_hands_on/blob/master/advanced/time_series_anomaly_detect_keras.ipynb

ここからコードに関する記述になります。

前処理

前処理でLSTMもしくはGRUで処理できるようにwindowごとにデータを分けて設定。正規化をしてモデルの学習がスムーズに行えるようにしました。また今回使用したwindowのサイズは3になっています。

window幅ごとにデータを分けて用意する関数

def get_data(data, time_steps: int=3):
    dataX = []
    print(data.shape)
    for i in range(len(data) - time_steps - 1):
        x = data[i:(i + time_steps), :]
        dataX.append(x)
    return np.array(dataX)

学習をしやすくするため正規化処理と正規化前の状態に戻す関数

def transform_data(original_data: np.array, inverse_option: bool, scaler: object):
    data_shape = original_data.shape
    data = original_data.reshape(-1, 1)
    if inverse_option is True:
        print('before max {}'.format(max(data)))
        print('Inverse')
        data = scaler.inverse_transform(data)
        print('after max {}'.format(max(data)))
    else:
        print('before max {}'.format(max(data)))
        print('Normalize')
        data = scaler.fit_transform(data)
        print(max(data))
        print('after max {}'.format(max(data)))
    data = data.reshape(data_shape)
    return data, scaler

上記の処理をまとめて行う関数

def prepare_data(original_data, time_steps):
    copy_data = original_data.copy()
    scaler = MinMaxScaler(feature_range=(0, 1), copy=False)
    data, scaler = transform_data(original_data=copy_data, 
                              inverse_option=False, scaler=scaler)
    data = np.asarray(data)
    data = data.reshape(-1, 1)
    x = get_data(data, time_steps=time_steps)
    return x, scaler

モデル定義部

create_modelでモデルを作成しています。

• timestepsの幅(windowの幅と同義)
• ノードの数
• optimizerで設定したいoptimizerを指定できます。デファオルトではadamが入っています。

今回使用するデータは1件のためバッチサイズに関連するパラメータは指定できません。

def create_model(input_dim,
                 time_steps,
                 latent_dim,
                 # データが一つしかないので1しか選べない
                 batch_size=1,
                 model_option='lstm',
                 optimizer='adam'
                ):
    x = Input(shape=(time_steps, input_dim,))

    if model_option == 'lstm':
        h = LSTM(latent_dim, stateful=False, return_sequences=True)(x)
    elif model_option == 'gru':
        h = GRU(latent_dim, stateful=False, return_sequences=True)(x)

    out = Dense(input_dim)(h)

    model = Model(x, out)
    model.summary()

    model.compile(optimizer=optimizer, loss='mean_squared_error', metrics=['mse'])

    return model

学習部

先ほど定義したモデルを使用して学習を行います。

model = create_model(input_dim, 
                     time_steps=time_steps,
                     latent_dim=120,
                     model_option='lstm')
model.fit(x, x, epochs=200)

学習が上手く動作すると下記のようになります。

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_2 (InputLayer)         (None, 3, 1)              0         
_________________________________________________________________
lstm_2 (LSTM)                (None, 3, 120)            58560     
_________________________________________________________________
dense_2 (Dense)              (None, 3, 1)              121       
=================================================================
Total params: 58,681
Trainable params: 58,681
Non-trainable params: 0
_________________________________________________________________
Epoch 1/200
296/296 [==============================] - 1s 2ms/step - loss: 0.1824 - mean_squared_error: 0.1824
Epoch 2/200
296/296 [==============================] - 0s 145us/step - loss: 0.0979 - mean_squared_error: 0.0979
:

実データと予測データの確認

下記の関数で実データと予測データの差異を確認しています。

def predict_model_show_graph(day, x, scaler, model):
    prepare_value = x.copy()
    preds = model.predict(prepare_value)

    x_scale, scaler = transform_data(original_data=prepare_value, inverse_option=True, scaler=scaler)
    predict_scale, scaler = transform_data(original_data=preds, inverse_option=True, scaler=scaler)

    plt.figure(figsize=(14, 8))
    plt.plot(day, x_scale[:, 0, 0], color='r', label='data')
    plt.plot(day, predict_scale[:, 0, 0], color='b', label='predict')
    plt.legend()
    plt.show()
    return predict_scale, x_scale

下記は予測データと実測データの一例です。

• 赤：実測データ
• 青：予測データ

異常度の計算部分の実装

異常度の計算は前回のブログをご覧ください。ただし分散は解析的に求められないので学習データで導出した分散を使用しています。
また異常度を計算する際は正規化した値を元に戻して予測値と実測値の差が小さくならないようにしています。(正規化した値で計算すると分散が非常に小さくなり、異常度の計算の際に分散で割る処理を行って異常度が高くなりすぎるため)

def calculate_mse(value, predict_value, variance=1.0):
    value = value[:, 0, 0]
    predict_value = predict_value[:, 0, 0]
    mse_value = [(v - p_v)**2 / variance for v, p_v in zip(value, predict_value)]
    return np.array(mse_value)

閾値の設定

閾値の設定のアプローチは複数あると思いますが今回は2点紹介します。

• 検証データの最大値を設定することで実測と予測とのずれをできるだけ許容するアプローチ
• 学習、検証データにおける異常度の平均と標準偏差を導出して、標準偏差の3倍以内(99.7%のデータが含まれると仮定)が正常データであると仮定して設定するアプローチ

今回は検証データの最大値を閾値として設定します。

mse_value_valid = calculate_mse(x_scale_valid, predict_valid, mse_value_variance)

threshold = np.max(mse_value_valid)

結果

実験条件

• LSTM
  • ノード数：120
    他のパラメータはkearasで提供されているデフォルト値
• GRU
  • ノード数：120
    他のパラメータはkearasで提供されているデフォルト値
• Optimiser
  • adam
    他のパラメータはkearasで提供されているデフォルト値
• epoch
  • 200

上記のモデルにより下記の環境で比較検証しました。

• 実行環境
  • OS: macOS Sierra
  • CPU: 2.9 GHz Intel Core i7
  • メモリー: 16 GB 2133 MHz LPDDR3
• pythonバージョン
  • 3.6.0
• ライブラリ

 numpy==1.14.2
ipython==6.2.1
notebook==5.4.1
pandas==0.22.0
statsmodels==0.8.0
matplotlib==2.2.2
lxml==4.2.0
bs4==0.0.1
scikit-learn==0.19.1
scipy==1.0.0
keras==2.1.5
tensorflow==1.7.0

各異常ケースにおける異常度の検出

下記はLSTMで異常スコアを導出したケース

• 正常データ
  • 検証データで設定した閾値を超えていない

• スパイク
  • 異常部分以外も超えてしまっている

• 波形変化
  • 波形変化部分の異常が捉えられている

• レベルシフト
  • シフトした部分以外の異常も出てしまっている

何となく異常を検知できている部分もあるという認識程度しかできないので異常度の性能を計る指標としてROC AUC:Receiver operating characteristic Area Under the curveを使用します。
ROC AUCの値が大きければ大きいほど良い性能を出しています。ROC AUCはROC curveの右下の面積になります。この面積が大きいほど異常検知性能が高いことを意味しています。
詳細な内容を把握したい方はWikipediaをご覧ください。

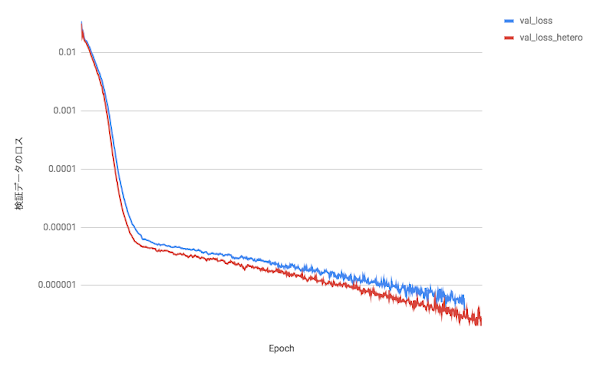
各手法による結果

図の右下にあるarea = {数値}の部分がROC AUCの値になります。

LSTM

GRU

この結果よりLSTMの方が若干、性能が良いことが確認できます。
モデルのフィッティグ性能が良いのですが異常の検知性能はあまりよくありません。そこで正常データの異常スコアの分布と異常データのスコアの分布を確認してみます。(LSTMの正規分布)

正常データの異常スコアの分布(縦軸：密度、横軸：異常度)

異常データの異常スコアの分布(縦軸：密度、横軸：異常度)

異常データの異常スコアの平均値11.95と正常データの異常スコアの平均値88.17は離れていますが分散が異常データの場合は大きく、重なっている部分が多くなり、分類性能が下がっていると思われます。
ここから3つの仮説ができます。

• 学習データのスムージングなどの処理をしていないのでノイズを含んだ状態で学習したため、異常データに対してもフィッティングするケースが発生し異常データの分布の分散が大きく広がった
• 正常データの特徴のみ学習するように前処理をかけて特徴だけ抽出すべきだった（情報落ちするのでデメリットも存在）
• スパイク型の異常は閾値設定でも十分に検知できるので他のタイプの異常を検知できるように検証すべきだった

上記の仮説を解決すれば精度が上がるかもしれません。興味がある方は上記の仮説が正しいかどうか確認してみてください。もしくは弊社のWantedlyから「話を聞きに行きたい」のボタンを押して貰った一緒に議論できると嬉しいです。

おまけ

高速化

GPU対応のCuDNNLSTM, CuDNNGRUがKerasでは用意されています。こちらは学習、予測がGPU環境でしか動作しませんがGPU環境で予測まで可能であればCuDNNLSTM, CuDNNGRUを使用する方がベターです。

CuDNNGRU
CuDNNLSTM

ハイパーパラメータチューニング

人手で全てのパラメータを調整するのは無駄なので予めパラメータの候補が絞れている場合は下記のライブラリを使用するとハイパーパラメータを変更しながらモデルを学習することが可能です。

GPyOpt

最後に

弊社では異常検知以外にも物体検出、3次元データ検索エンジンの開発をしています。これらに興味があるエンジニアがいらっしゃれば絶賛採用中なので是非、弊社へ応募してください。

参考

入門 機械学習による異常検知―Rによる実践ガイド

Recurrent Neural Network Tutorial, Part 4 – Implementing a GRU/LSTM RNN with Python and Theano