【深層学習】時系列データに対する１次元畳み込み層の出力を可視化

2018/07/19

機械学習エンジニアインターン生の杉崎です。今回は時系列データ予測に一次元畳み込み層を使用した際の出力の可視化の方法について書きたいと思います。

本記事の目的

　深層学習における畳込み層は多くは画像等の２次元データに使われることが多いです。そして、ブラックボックスであるモデルに対して理由を明らかにするため、中間層の重みや出力を取り出し可視化する様々な手法が提案されています。(下図)

画像引用元

　しかし、そんな中で一次元畳込み層(Conv1D)を用いたモデルでは可視化の事例があまり多くありません。そこで今回はConv1D層の出力の可視化の一例についてご紹介します。

本記事の目的
- 画像などの２次元データに対する可視化手法は数多く提案されている。
- しかし、１次元データに対する中間層の可視化は事例が少ない。
- そこで、１次元データを入力とする１次元畳み込み層(Conv1D)を使用したモデルを用いて可視化を行う。
実装環境
ソースコード
サンプル時系列データの作成
一次元畳み込み層を用いた時系列予測モデル作成
- 入力データの前処理
- 予測モデル作成 (Keras)
- モデルの学習
- 学習済みモデルの保存
- 学習過程の確認
- 予測の確認
中間層Conv1Dの出力を取得と可視化
- 学習済みモデルの読み込み
- 入力データ作成
- 中間層の出力の取得方法
- conv1d_1(Conv1D)の出力の描画
- チャネル1の描画
- (batch, steps) で描画
- steps分を足しあわせて描画
- すべてのチャネルを入力波形と重ねて描画
- 各チャネルごとに入力波形と重ねて描画
特定のチャネルを削除した予測モデル
- ２つのチャネルを削除
- 正解波形と予測波形の比較
- MSE(二乗和誤差)のカラーマップ表示
最後に
参考

環境

OS : Ubuntu 16.04 LTS
Python : Python3.5.2
Jupyter
- jupyter 4.4.0
- jupyter-notebook 5.6.0

ソースコード

create_OnlyConv1dModel__SimpleSinFuncWithNoNoise.ipynb
- サンプル時系列データの作成
- 一次元畳み込み層を用いた時系列予測モデル作成
visualize_OnlyConv1dModel__SimpleSinFuncWithNoNoise.ipynb
- 中間層Conv1Dの出力を取得と可視化
getLastOutputByChangingHiddenOutput__OnlyConv1dModel__SimpleSinFuncWithNoNoise.ipynb
- 特定のチャネルを削除した予測モデル

※もしGitHub上でipynbが表示されない場合はnbviewerのサイトへリンクのURLをペーストしてください。

サンプル時系列データの作成

　今回使用するサンプル時系列データは正弦波です。

$\textbf{toyfunc(t)} = \sin\left( \frac{2\pi}{T} t \right)$

この関数を表すコードを以下に示します。

 def mySin(t, period=100):
    """
    時刻t, 周期period
    """
    return np.sin(2.0 * np.pi * t/period)
 
# Add Noise
def toy_func(tStart=0, tStop=100, tStep=1, noiseAmpl=0.05):
    """
    T : sin波の周期
    ampl : ノイズ振幅調整
    """
    t = np.arange(start=tStart, stop=tStop, step=tStep)
    noise = np.random.randn(t.shape[0])  # mean=0, standard_deviation=1
    return (t, mySin(t=t, period=100) + noiseAmpl * noise)

一次元畳み込み層による時系列予測モデル作成

　まず時系列予測を行うConv1dを用いた学習済みモデルが必要なので、サンプルデータとモデルの学習を行います。ソースコードはこちらです。

入力データの前処理

　次にモデルに入力する形に変えてやります。ここで行おうとしているは過去100個分のデータ(steps100)を用いてその一つ先のデータを予測する(予測サイズ1)というものです。以下のGIF動画の示すようにモデルの学習時に与えるデータを入力データと正解データに分けます。 (各ブロックの数字はデータのインデックスです。)

<br>
　この処理を行っているコードが以下になります。プログラムの中ではstepsの箇所をwindowsizeという変数を用いています。

 >>> #----------------------------------------
>>> # Parameters
>>> #----------------------------------------
>>> windowsize = 100  # 周期と同じくとる
>>> predictsize = 1
>>> sample_data_size = 10000
>>> wave_size = sample_data_size
>>> trainsize = int(10000*0.8)
 
>>> #----------------------------------------
>>> # Sample Wave
>>> #----------------------------------------
>>> t, sample_wave = toy_func(tStop=sample_data_size, noiseAmpl=0)
>>> print(sample_wave.shape)
(10000,)
 
>>> #----------------------------------------
>>> # create input data
>>> #----------------------------------------
>>> input_data  = np.empty(shape=(0, windowsize))
>>> output_data = np.empty(shape=(0, predictsize))
>>> print(input_data.shape)
(0, 100)
>>> print(output_data.shape)
(0, 1)
>>> for i in range( sample_wave.shape[0] - (windowsize + predictsize) + 1 ):
        input_data = np.append(arr=input_data,
                               values=sample_wave[i:(i+windowsize)].reshape(1, -1),
                               axis=0)
        output_data = np.append(arr=output_data,
                                values=sample_wave[(i+windowsize):(i+windowsize+predictsize)].reshape(1, -1),
                                axis=0)
>>> print("input_data.shape  : ", input_data.shape)
input_data.shape  :  (9900, 100)
>>> print("output_data.shape : ", output_data.shape)
output_data.shape :  (9900, 1)
>>> #--------------------
>>> # Kerasのモデルに入力できる形にするためにreshapeして次元を足す
>>> #--------------------
>>> input_data = input_data.reshape((-1, windowsize, 1))
>>> output_data = output_data.reshape((-1, predictsize,))
>>> print("input_data.shape  : ", input_data.shape)
input_data.shape  :  (9900, 100, 1)
>>> print("output_data.shape : ", output_data.shape)
output_data.shape :  (9900, 1)
>>> train_x, test_x = input_data[:trainsize], input_data[trainsize:]
>>> train_y, test_y = output_data[:trainsize], output_data[trainsize:]
>>> print("train_x.shape : ", train_x.shape)
train_x.shape :  (8000, 100, 1)
>>> print("train_y.shape : ", train_y.shape)
train_y.shape :  (8000, 1)
>>> print("test_x.shape  : ", test_x.shape)
test_x.shape  :  (1900, 100, 1)
>>> print("test_y.shape  : ", test_y.shape)
test_y.shape  :  (1900, 1)

予測モデル作成 (Keras)

　今回はConv1Dを用いた小さめのモデルを作成します。
　入力や各層の出力の形は(batch, steps, channels)のように表されますが、入力のstepsを維持しています。

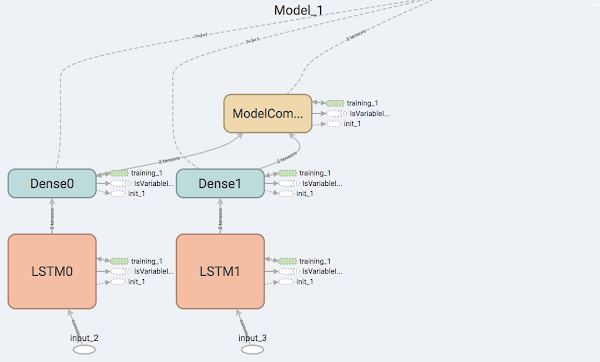
 >>> from keras.models import Sequential
>>> from keras.layers.convolutional import Conv1D
>>> from keras.layers.pooling import GlobalMaxPooling1D
 
>>> channel_size = 8
>>> kernel_size = 10
 
>>> model = Sequential()
>>> model.add( Conv1D(filters=channel_size, kernel_size=kernel_size,
                      strides=1, padding="same", activation="relu",
                      input_shape=(windowsize, 1) ) )
>>> model.add( Conv1D(filters=1, kernel_size=8, padding='same', activation='tanh' ) )
>>> model.add( GlobalMaxPooling1D() )
 
>>> model.compile(loss='mse', optimizer='adam')
>>> model.summary()
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv1d_1 (Conv1D)            (None, 100, 8)            88        
_________________________________________________________________
conv1d_2 (Conv1D)            (None, 100, 1)            65        
_________________________________________________________________
global_max_pooling1d_1 (Glob (None, 1)                 0         
=================================================================
Total params: 153
Trainable params: 153
Non-trainable params: 0
_________________________________________________________________
>>> from keras.utils import plot_model
>>> file = str(plot_images_Path / "model.png")
>>> plot_model(model=model, to_file=file)
>>> from IPython.display import SVG
>>> from keras.utils.vis_utils import model_to_dot
>>> SVG(data=model_to_dot(model).create(prog='dot', format='svg'))

　イメージとしては以下の図のようになります。色の付いているconv1d_1は後ほど可視化する対象です。

モデルの学習

　それではこのモデルを学習して保存します。model.save()のoverwriteをFalseにすると同じ名前のファイルが存在しているとき上書きするかを確認するようになります。

 >>> #--------------------
>>> #  Fit
>>> #--------------------
>>> epochs = 100
>>> from keras.callbacks import EarlyStopping
>>> earlystop = EarlyStopping(monitor='val_loss', min_delta=0, patience=5, verbose=1, mode='auto')
>>> callbacks_list = [earlystop]
>>> history = model.fit(x=train_x,
                        y=train_y,
                        epochs=epochs,
                        verbose=1,
                        validation_split=0.1,
                        callbacks=callbacks_list)
>>> #--------------------
>>> #  Save Model
>>> #--------------------
>>> modelpath = str(keras_model_h5_Path / "model__{}_kernelsize{}.h5".format(ipynb_title, kernel_size))
>>> model.save(filepath=modelpath, overwrite=False)

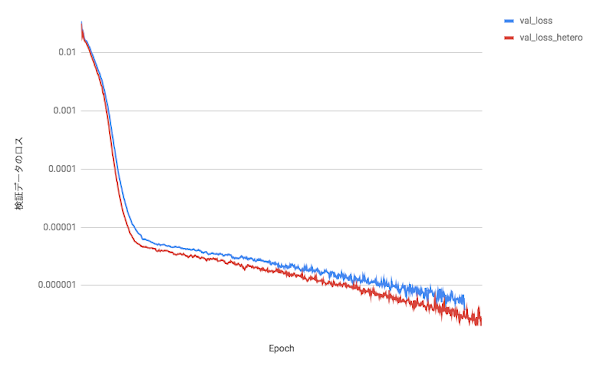
学習過程の確認

　下図はepochsを重ねるごとのlossの値です。学習データに対するlossとバリデーションデータに対するlossがともに収束しているため、上手く学習できています。

　正解波形と予測波形を比較してもある程度予測出来ています。

中間層Conv1Dの出力を取得と可視化

　モデルの学習が終わりましたのでこのモデルで使用したConv1D層のどのチャネルが、波形のどの部分に強く反応しているのかを可視化してみます。

学習済みモデルの読み込み

　それでは先ほど保存したモデルを読み込みます。

 >>> from keras.models import load_model
>>> model_filename = "model__create_OnlyConv1dModel__SimpleSinFuncWithNoNoise_kernelsize10.h5"
>>> modelpath = str(keras_model_h5_Path / model_filename)
>>> model = load_model(filepath=modelpath)
>>> model.summary()
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv1d_1 (Conv1D)            (None, 100, 8)            88        
_________________________________________________________________
conv1d_2 (Conv1D)            (None, 100, 1)            65        
_________________________________________________________________
global_max_pooling1d_1 (Glob (None, 1)                 0         
=================================================================
Total params: 153
Trainable params: 153
Non-trainable params: 0
_________________________________________________________________

入力データの作成と処理

　conv1d_1 (Conv1D)の出力を得るためには一度データを入力する必要がありますので、学習に使用したものと同様に波形を作成します。学習ではt=0〜9,999のデータを使いましたので、ここで入力するデータはt=10,000〜10,300とします。
　波形サイズ:300、ステップサイズ:100、予測サイズ:1の入力データとします。

 >>> tStart = 10000
>>> windowsize = 100
>>> predictsize = 1
>>> wave_size = 300
>>> assert wave_size - windowsize > windowsize  # 後の畳み込むコードではこの条件が必要
 
>>> #----------------------------------------
>>> # create a wave
>>> #----------------------------------------
>>> t, wave = toy_func(tStart=tStart, tStop=tStart+wave_size, noiseAmpl=0)
 
>>> #----------------------------------------
>>> # create input data
>>> #----------------------------------------
>>> input_arr = np.empty(shape=(0, windowsize))
>>> print(input_arr.shape)
(0, 100)
>>> for i in range( wave.shape[0] - (windowsize + predictsize) + 1 ):
>>>     input_arr = np.append(arr=input_arr,
>>>                            values=wave[i:(i+windowsize)].reshape(1, -1),
>>>                            axis=0)
>>> print("input_arr.shape  : ", input_arr.shape)
input_arr.shape  :  (200, 100)
>>> input_arr = input_arr.reshape((-1, windowsize, 1))
>>> print("input_arr.shape  : ", input_arr.shape)
input_arr.shape  :  (200, 100, 1)

中間層の出力の取得方法

　詳しくはKerasのドキュメントを参照してください。ここでは以下のような手法で取得しています。例としてconv1d_1(Conv1D)の出力を取得しています。

 >>> from keras import backend as K
>>> get_hidden_layer_model = K.function(inputs=[model.input],
                                        outputs=[model.layers[0].output])
>>> hidden_layer_output = get_hidden_layer_model(inputs=[input_arr])[0]
>>> print(hidden_layer_output.shape)
(200, 100, 8)

`conv1d_1(Conv1D)`の出力の描画

　conv1d_1(Conv1D)の出力を(batch, steps, channels)=(200, 100, 8)の形で取得出来たので、このデータをチャネルごとに分けて描画してみます。値の大きさはカラーマップで区別するのが良いと思います。

チャネル1の描画

　それでは例として8つのチャネル(ch0-ch7)のうち、ch1の描画を行います。ちなみにch1を取り上げた理由は見た目が分かりやすかったからです。最終的にはすべて描画します。

(batch, steps) で描画

　最初はconv1d_1(Conv1D)の出力からch1のみを取り出したもの((batch, steps, channels)=(200, 100, 1))をそのまま描画します。(x軸, y軸)=(batch, steps)のようにとれば問題無さそうです。

 >>> ch = 1
>>> assert ch < hidden_layer_output.shape[2]
>>> #--------------------
>>> # Resize
>>> #--------------------
>>> outputs = hidden_layer_output[:, :, ch].squeeze()
>>> print(outputs.shape)
(200, 100)
>>> outputs = outputs.T
>>> print(outputs.shape)
(100, 200)
>>> #--------------------
>>> # get max value for plot Color
>>> #--------------------
>>> #    カラーマップでは値が0に近づくほど無色にしたほうがわかりやすいため, 
>>> #    最大値と最小値の絶対値のうち最大をとり, それを両極端の色とする.
>>> print("max : ", np.max(outputs))
max :  3.1358464
>>> print("min : ", np.min(outputs))
min :  0.0
>>> max_abs = np.maximum(np.max(outputs),
                         abs(np.min(outputs))
                        )
>>> print("max abs : ", max_abs)
max abs :  3.1358464
 
>>> #--------------------------------------------------------------------------------
>>> # Setting Parameter
>>> #--------------------------------------------------------------------------------
>>> title = "{}__channel{}__allWindow__windowsize_{}".format(ipynb_title, ch, windowsize)
>>> filename = title + ".png"
 
>>> ##------------------------------------------------------------
>>> ## Plot
>>> ##------------------------------------------------------------
>>> figsize=(14, 7)
>>> fig = plt.figure(figsize=figsize)
>>> ax = fig.add_subplot(1,1,1)
>>> mappable = ax.imshow(outputs,
                         cmap='seismic',  # <-- (min,max)=(blue, red)
                         vmin=-max_abs,
                         vmax=max_abs,
                         )
>>> fig.colorbar(mappable,
                 ax=ax,
                 #orientation='horizontal',
                 orientation='vertical',
                 shrink=0.5,
                 )
 
>>> ###----------------------------------------
>>> ### change x,y axis ratio
>>> ###----------------------------------------
>>> ### height is aspect_num times the width
>>> ### 縦:横=1:2
>>> print("ax.get_xlim() : {}".format(ax.get_xlim()))
ax.get_xlim() : (-0.5, 199.5)
>>> print("ax.get_ylim() : {}".format(ax.get_ylim()))
ax.get_ylim() : (99.5, -0.5)
>>> xratio = 6
>>> aspect = (1/xratio) * (ax.get_xlim()[1] - ax.get_xlim()[0]) / (ax.get_ylim()[0] - ax.get_ylim()[1])
>>> ax.set_aspect(aspect=aspect)
 
>>> ###----------------------------------------
>>> ### plot config
>>> ###----------------------------------------
>>> ax.set_title(label=title, fontsize=20, y=1.5)
>>> ax.set_xlabel(xlabel="t'", fontsize=15)
>>> ax.set_ylabel(ylabel="windowsize index", fontsize=15, rotation=0)
>>> ax.yaxis.set_label_coords(x=0.01, y=1.1)  # ylabel position
>>> ax.tick_params(labelsize=20)  # tick fontsize
 
>>> fig.savefig(fname=str(plot_images_Path / filename))
>>> plt.show()

　この結果より右上から左下に同じくらいの値が並んでいます。これはモデル定義の際にConv1Dのstridesの値がデフォルトで1になっているからです。各stepが入力として渡した時系列を1つずつずらして畳み込みフィルタに入れているためです。
　もう少し詳しく説明します。以下のGIFは入力データ((batch, steps, channels)=(200, 100, 1))を(batch, steps)=(200, 100)の行列とみた配列です。四角の中の数字が波形のインデックスであり、カラーマップ同様、右上から左下に同じインデックスが並んでいます。

　この入力データが kernelsize=10, strides=1, padding="same" の畳み込みフィルタを通る様子が以下のGIFになります(このときのpaddingは入力データの左右に5個ずつデータを加えると出力サイズが同じ(same)になります)。つまり、フィルタを通ったあとのデータは右上から左下にかけて同じ波形のデータを入力とした出力になります。これが先ほどのカラーマップの特徴の理由です。 (正確に言えば、両端の、パディングを含んでいる箇所の畳み込みは取り込むパディングの数が違うので一致はしませんが近い値になります。)

steps分を足しあわせて描画

　上の結果を見る限り各stepsを別々に考えることにはあまり意味はありません。そこで斜めの値の和あるいは平均などの形で一つにまとめます。ここではsteps分を足しあわせて一つの値にしています。今回は和を取ってまとめようと思いますが、以下の図のオレンジの箇所は足りないので値を複製して埋めます(詳細はコードを確認してください)。プログラムでは畳み込みの出力(行列)を転置して扱ったほうがわかりやすいため転置されていることに注意してください。

プログラムコードは以下のように書くことで steps を一つにまとめることができます。

 >>> figsize = (25, 10)
>>> cmap = "seismic"
 
>>> #--------------------------------------------------------------------------------
>>> # Setting Parameter
>>> #--------------------------------------------------------------------------------
>>> title = "{}__channel{}__convolveWindows__windowsize_{}".format(ipynb_title, ch, windowsize)
>>> filename = title + ".png"
 
>>> #----------------------------------------
>>> # Convolved window size
>>> #----------------------------------------
>>> outputs_tmp = hidden_layer_output[:, :, ch].squeeze()
>>> outputs_tmp = outputs_tmp.T
 
>>> # Prepare for convolved
>>> outputs = np.empty(shape=(0, wave_size - predictsize))
>>> for window_idx in range(windowsize):
        _shape = outputs_tmp.shape[1]
        # append last
        if window_idx < windowsize-1:
            _val = outputs_tmp[-1, -windowsize+window_idx+1:]
            insert_arr = np.append(arr=outputs_tmp[window_idx],
                                   values=_val,
                                   axis=None)
        else:
            insert_arr = outputs_tmp[window_idx]
 
        # insert first
        _val = outputs_tmp[0, :window_idx]
        insert_arr = np.insert(arr=insert_arr,
                               obj=[0 for i in range(window_idx)],
                               values=_val,
                               ).reshape(1, -1)
        # append to the array
        #print(outputs.shape)
        #print(insert_arr.shape)
        outputs = np.append(
            arr=outputs,
            values=insert_arr,
            axis=0,
        )
>>> print("outputs.shape : ", outputs.shape)
outputs.shape :  (100, 299)
 
>>> # Convolved
>>> outputs_convolve_windows = outputs.sum(axis=0).reshape(1, -1)
>>> print("outputs_convolve_windows.shape : ", outputs_convolve_windows.shape)
outputs_convolve_windows.shape :  (1, 299)

　steps を一つにまとめたあと(outputs_convolve_windows) では、100だったstepsが1になっていることがわかります。これを描画したものが下図です。

　横軸は0-298の299個あり、これは入力に使用した0-298の波形データ数と一致させています。これより元の波形と重ねて表示することができます。(下図)

すべてのチャネルを入力波形と重ねて描画

　他のチャネルについても表示します。(下図)
　全体を表示してみると ch0 と ch7 がほとんど寄与していないことがわかります。また、各チャネルごとに波形のなかで注目している箇所が異なることもわかると思います。

各チャネルごとに入力波形と重ねて描画

　具体的にどの箇所でどのチャネルが反応しているのかをわかりやすくなるように分けて描画します(下図)。すると、いくつかの特徴を把握できます。
– ch0,ch7 の反応はかなり小さい
– ch1 の反応は正弦波の山で特に大きい
– ch3 は降下箇所での反応が大きい
– ch4 は上昇箇所での反応が大きい
– ch5, ch6 は谷付近で反応

特定のチャネルを削除した予測モデル

　今まででの方法では中間層の出力値からどのチャネルの出力値が高いかということしかわかりません。そこで具体的にどのチャネルが重要であるかを判定するために、あるチャネルを削除したときのMSE(二乗和誤差)の利用を考えてみます。特定のチャネルを削除するということは、中間層における出力から特定のチャネルの値をすべて0にして次の層に渡すことであるとみなすことができます。
　今回は以下のようにconv1d_1(Conv1D)の出力のチャネルを削除して次の層に渡しています。

2つのチャネルを削除

　8チャネルのうち2つのチャネルの削除する場合の数は28通りなので全組み合わせについて試してみます。正解波形と予測波形の比較とMSE(二乗和誤差)のカラーマップ表示を行います。

　以下の関数はchannel_indexに与えたチャネルを取り除いた結果を返してくれます。

 def removeIntermidiateChannels(input_array, model, layer_index=0, channel_index=[0]):
    """
    model : keras model
    layer_index : int
        層の順番
    channel_index=[]
        削除するチャネル
    reference:
      - https://keras.io/getting-started/faq/#how-can-i-obtain-the-output-of-an-intermediate-layer
    """
    from keras import backend as K
 
    # check input
    assert type(model) == keras.models.Sequential
    assert type(layer_index) == int
    assert type(channel_index) == list 
 
    # get first half layers output
    get_first_half = K.function(inputs=[model.input],
                                outputs=[model.layers[layer_index].output])
    first_half_output = get_first_half(inputs=[input_array])[0]
 
    # remove channels
    shape = first_half_output.shape[:2]
    for idx in channel_index:
        first_half_output[:,:,idx] = np.zeros(shape)
 
    # get second half layers output
    get_second_half = K.function(inputs=[model.layers[layer_index+1].input],
                                 outputs=[model.output])
    second_half_output = get_second_half(inputs=[first_half_output])[0]
    return second_half_output

正解波形と予測波形の比較

　チャネルを削除したモデルによる予測波形を正解波形と並べて描画してみます。

 >>> channels_num = int(model.layers[0].output.shape[2])
 
>>> mse_remove2ch = np.zeros((channels_num, channels_num))
>>> mse_remove2ch.shape
(8, 8)
 
>>> fig = plt.figure(figsize=(50, 50))
>>> for ch1 in range(channels_num):
        for ch2 in range(channels_num):
            if ch1 == ch2:
                ax = fig.add_subplot(channels_num, channels_num, ch1*channels_num+ch2+1)
                #ax.plot(t, t)
            else:
                ax = fig.add_subplot(channels_num, channels_num, ch1*channels_num+ch2+1)
                ax.plot(t, wave)
                last_layer_output = removeIntermidiateChannels(input_array=input_arr,
                                                               model=model,
                                                               layer_index=0,
                                                               channel_index=[ch1, ch2])
                ax.plot(t[-len(last_layer_output):], last_layer_output.squeeze())
                mse = mean_squared_error(y_true=wave[windowsize:], y_pred=last_layer_output)
                ax.set_title(label="(ch{}, ch{})'s, MSE : {}".format(ch1, ch2, mse))
                mse_remove2ch[ch1, ch2] = mse
>>> plt.show()

これらの図は全体で、左から順にch0-ch7を、上から順にch0-ch7を削除したものです。よって、右上と左下の図は対称的になっています。

拡大図リンク

　これにより視覚的にずれの大きいものやずれ方の特徴などをつかむことができます。 よりズレが大きいほどそのとき削除したチャネルの役割が大きかったと言えます。

MSE(二乗和誤差)のカラーマップ表示

　視覚的情報だけではズレを正しく判断できないときがあるので、評価指標としてMSE(二乗和誤差)を用います。先ほどの描画の際にmse_remove2chにMSEの値を保存しておいたのでカラーマップ表示によってMSEの大きいものをすぐに確認できます。

 >>> #--------------------
>>> #  get max value for plot Color
>>> #--------------------
>>> max_abs = np.max(mse_remove2ch)
>>> print("max abs : ", max_abs)
max abs :  0.4231775843779829
 
>>> #------------------------------------------------------------
>>> #  Plot
>>> #------------------------------------------------------------
>>> figsize = None
>>> fontsize = 20
 
>>> fig = plt.figure(figsize=figsize)
>>> ax = fig.add_subplot(1,1,1)
>>> mappable = ax.imshow(mse_remove2ch,
                         cmap='seismic',  # <-- (min,max)=(blue, red)
                         vmin=-max_abs,
                         vmax=max_abs,
                         )
>>> fig.colorbar(mappable,
                 ax=ax,
                 orientation='vertical',
                 shrink=1.0,
                 )
>>> ax.set_title(label="MSE", fontsize=fontsize)
>>> ax.set_xticks(ticks=np.arange(channels_num))
>>> ax.set_yticks(ticks=np.arange(channels_num))
>>> ax.set_xlabel(xlabel="ch2", fontsize=fontsize)
>>> ax.xaxis.set_label_coords(x=1.0, y=-0.1)
>>> ax.set_ylabel(ylabel="ch1", fontsize=fontsize, rotation=0)
>>> ax.yaxis.set_label_coords(x=0, y=1.02)
>>> ax.tick_params(labelsize=fontsize)
>>> plt.show()

　この結果よりMSEが大きいペアである(ch1, ch3), (ch2, ch3)の重要度が高く、全体的にはch3が大きく寄与していることが把握できます。

最後に

　本記事では一次元畳み込み層(Conv1D)の可視化手法について扱いました。大きく分けて出力の可視化とチャネルを削除することによる重要度の把握しました。深い層のモデルについては挑戦中ですが、入力層に近い層に関してはこれらの方法が役にたつと思います。ソースコードへのリンクも載せましたので、ぜひコードを参考にしてみてください。

【深層学習】時系列データに対する１次元畳み込み層の出力を可視化

本記事の目的

目次

環境

ソースコード

サンプル時系列データの作成

一次元畳み込み層による時系列予測モデル作成

入力データの前処理

予測モデル作成 (Keras)

モデルの学習

学習過程の確認

中間層Conv1Dの出力を取得と可視化

学習済みモデルの読み込み

入力データの作成と処理

中間層の出力の取得方法

`conv1d_1(Conv1D)`の出力の描画

チャネル1の描画

(batch, steps) で描画

steps分を足しあわせて描画

すべてのチャネルを入力波形と重ねて描画

各チャネルごとに入力波形と重ねて描画

特定のチャネルを削除した予測モデル

2つのチャネルを削除

正解波形と予測波形の比較

MSE(二乗和誤差)のカラーマップ表示

最後に

参考

その他の記事

関連職種

	def mySin(t, period=100):
	"""
	時刻t, 周期period
	"""
	return np.sin(2.0 * np.pi * t/period)

	# Add Noise
	def toy_func(tStart=0, tStop=100, tStep=1, noiseAmpl=0.05):
	"""
	T : sin波の周期
	ampl : ノイズ振幅調整
	"""
	t = np.arange(start=tStart, stop=tStop, step=tStep)
	noise = np.random.randn(t.shape[0]) # mean=0, standard_deviation=1
	return (t, mySin(t=t, period=100) + noiseAmpl * noise)

	>>> #----------------------------------------
	>>> # Parameters
	>>> #----------------------------------------
	>>> windowsize = 100 # 周期と同じくとる
	>>> predictsize = 1
	>>> sample_data_size = 10000
	>>> wave_size = sample_data_size
	>>> trainsize = int(10000*0.8)

	>>> #----------------------------------------
	>>> # Sample Wave
	>>> #----------------------------------------
	>>> t, sample_wave = toy_func(tStop=sample_data_size, noiseAmpl=0)
	>>> print(sample_wave.shape)
	(10000,)

	>>> #----------------------------------------
	>>> # create input data
	>>> #----------------------------------------
	>>> input_data = np.empty(shape=(0, windowsize))
	>>> output_data = np.empty(shape=(0, predictsize))
	>>> print(input_data.shape)
	(0, 100)
	>>> print(output_data.shape)
	(0, 1)
	>>> for i in range( sample_wave.shape[0] - (windowsize + predictsize) + 1 ):
	input_data = np.append(arr=input_data,
	values=sample_wave[i:(i+windowsize)].reshape(1, -1),
	axis=0)
	output_data = np.append(arr=output_data,
	values=sample_wave[(i+windowsize):(i+windowsize+predictsize)].reshape(1, -1),
	axis=0)
	>>> print("input_data.shape : ", input_data.shape)
	input_data.shape : (9900, 100)
	>>> print("output_data.shape : ", output_data.shape)
	output_data.shape : (9900, 1)
	>>> #--------------------
	>>> # Kerasのモデルに入力できる形にするためにreshapeして次元を足す
	>>> #--------------------
	>>> input_data = input_data.reshape((-1, windowsize, 1))
	>>> output_data = output_data.reshape((-1, predictsize,))
	>>> print("input_data.shape : ", input_data.shape)
	input_data.shape : (9900, 100, 1)
	>>> print("output_data.shape : ", output_data.shape)
	output_data.shape : (9900, 1)
	>>> train_x, test_x = input_data[:trainsize], input_data[trainsize:]
	>>> train_y, test_y = output_data[:trainsize], output_data[trainsize:]
	>>> print("train_x.shape : ", train_x.shape)
	train_x.shape : (8000, 100, 1)
	>>> print("train_y.shape : ", train_y.shape)
	train_y.shape : (8000, 1)
	>>> print("test_x.shape : ", test_x.shape)
	test_x.shape : (1900, 100, 1)
	>>> print("test_y.shape : ", test_y.shape)
	test_y.shape : (1900, 1)

	>>> from keras.models import Sequential
	>>> from keras.layers.convolutional import Conv1D
	>>> from keras.layers.pooling import GlobalMaxPooling1D

	>>> channel_size = 8
	>>> kernel_size = 10

	>>> model = Sequential()
	>>> model.add( Conv1D(filters=channel_size, kernel_size=kernel_size,
	strides=1, padding="same", activation="relu",
	input_shape=(windowsize, 1) ) )
	>>> model.add( Conv1D(filters=1, kernel_size=8, padding='same', activation='tanh' ) )
	>>> model.add( GlobalMaxPooling1D() )

	>>> model.compile(loss='mse', optimizer='adam')
	>>> model.summary()
	_________________________________________________________________
	Layer (type) Output Shape Param #
	=================================================================
	conv1d_1 (Conv1D) (None, 100, 8) 88
	_________________________________________________________________
	conv1d_2 (Conv1D) (None, 100, 1) 65
	_________________________________________________________________
	global_max_pooling1d_1 (Glob (None, 1) 0
	=================================================================
	Total params: 153
	Trainable params: 153
	Non-trainable params: 0
	_________________________________________________________________
	>>> from keras.utils import plot_model
	>>> file = str(plot_images_Path / "model.png")
	>>> plot_model(model=model, to_file=file)
	>>> from IPython.display import SVG
	>>> from keras.utils.vis_utils import model_to_dot
	>>> SVG(data=model_to_dot(model).create(prog='dot', format='svg'))

	>>> #--------------------
	>>> # Fit
	>>> #--------------------
	>>> epochs = 100
	>>> from keras.callbacks import EarlyStopping
	>>> earlystop = EarlyStopping(monitor='val_loss', min_delta=0, patience=5, verbose=1, mode='auto')
	>>> callbacks_list = [earlystop]
	>>> history = model.fit(x=train_x,
	y=train_y,
	epochs=epochs,
	verbose=1,
	validation_split=0.1,
	callbacks=callbacks_list)
	>>> #--------------------
	>>> # Save Model
	>>> #--------------------
	>>> modelpath = str(keras_model_h5_Path / "model__{}_kernelsize{}.h5".format(ipynb_title, kernel_size))
	>>> model.save(filepath=modelpath, overwrite=False)

	>>> from keras.models import load_model
	>>> model_filename = "model__create_OnlyConv1dModel__SimpleSinFuncWithNoNoise_kernelsize10.h5"
	>>> modelpath = str(keras_model_h5_Path / model_filename)
	>>> model = load_model(filepath=modelpath)
	>>> model.summary()
	_________________________________________________________________
	Layer (type) Output Shape Param #
	=================================================================
	conv1d_1 (Conv1D) (None, 100, 8) 88
	_________________________________________________________________
	conv1d_2 (Conv1D) (None, 100, 1) 65
	_________________________________________________________________
	global_max_pooling1d_1 (Glob (None, 1) 0
	=================================================================
	Total params: 153
	Trainable params: 153
	Non-trainable params: 0
	_________________________________________________________________

	>>> tStart = 10000
	>>> windowsize = 100
	>>> predictsize = 1
	>>> wave_size = 300
	>>> assert wave_size - windowsize > windowsize # 後の畳み込むコードではこの条件が必要

	>>> #----------------------------------------
	>>> # create a wave
	>>> #----------------------------------------
	>>> t, wave = toy_func(tStart=tStart, tStop=tStart+wave_size, noiseAmpl=0)

	>>> #----------------------------------------
	>>> # create input data
	>>> #----------------------------------------
	>>> input_arr = np.empty(shape=(0, windowsize))
	>>> print(input_arr.shape)
	(0, 100)
	>>> for i in range( wave.shape[0] - (windowsize + predictsize) + 1 ):
	>>> input_arr = np.append(arr=input_arr,
	>>> values=wave[i:(i+windowsize)].reshape(1, -1),
	>>> axis=0)
	>>> print("input_arr.shape : ", input_arr.shape)
	input_arr.shape : (200, 100)
	>>> input_arr = input_arr.reshape((-1, windowsize, 1))
	>>> print("input_arr.shape : ", input_arr.shape)
	input_arr.shape : (200, 100, 1)

	>>> from keras import backend as K
	>>> get_hidden_layer_model = K.function(inputs=[model.input],
	outputs=[model.layers[0].output])
	>>> hidden_layer_output = get_hidden_layer_model(inputs=[input_arr])[0]
	>>> print(hidden_layer_output.shape)
	(200, 100, 8)

	>>> ch = 1
	>>> assert ch < hidden_layer_output.shape[2]
	>>> #--------------------
	>>> # Resize
	>>> #--------------------
	>>> outputs = hidden_layer_output[:, :, ch].squeeze()
	>>> print(outputs.shape)
	(200, 100)
	>>> outputs = outputs.T
	>>> print(outputs.shape)
	(100, 200)
	>>> #--------------------
	>>> # get max value for plot Color
	>>> #--------------------
	>>> # カラーマップでは値が0に近づくほど無色にしたほうがわかりやすいため,
	>>> # 最大値と最小値の絶対値のうち最大をとり, それを両極端の色とする.
	>>> print("max : ", np.max(outputs))
	max : 3.1358464
	>>> print("min : ", np.min(outputs))
	min : 0.0
	>>> max_abs = np.maximum(np.max(outputs),
	abs(np.min(outputs))
	)
	>>> print("max abs : ", max_abs)
	max abs : 3.1358464

	>>> #--------------------------------------------------------------------------------
	>>> # Setting Parameter
	>>> #--------------------------------------------------------------------------------
	>>> title = "{}__channel{}__allWindow__windowsize_{}".format(ipynb_title, ch, windowsize)
	>>> filename = title + ".png"

	>>> ##------------------------------------------------------------
	>>> ## Plot
	>>> ##------------------------------------------------------------
	>>> figsize=(14, 7)
	>>> fig = plt.figure(figsize=figsize)
	>>> ax = fig.add_subplot(1,1,1)
	>>> mappable = ax.imshow(outputs,
	cmap='seismic', # <-- (min,max)=(blue, red)
	vmin=-max_abs,
	vmax=max_abs,
	)
	>>> fig.colorbar(mappable,
	ax=ax,
	#orientation='horizontal',
	orientation='vertical',
	shrink=0.5,
	)

	>>> ###----------------------------------------
	>>> ### change x,y axis ratio
	>>> ###----------------------------------------
	>>> ### height is aspect_num times the width
	>>> ### 縦:横=1:2
	>>> print("ax.get_xlim() : {}".format(ax.get_xlim()))
	ax.get_xlim() : (-0.5, 199.5)
	>>> print("ax.get_ylim() : {}".format(ax.get_ylim()))
	ax.get_ylim() : (99.5, -0.5)
	>>> xratio = 6
	>>> aspect = (1/xratio) * (ax.get_xlim()[1] - ax.get_xlim()[0]) / (ax.get_ylim()[0] - ax.get_ylim()[1])
	>>> ax.set_aspect(aspect=aspect)

	>>> ###----------------------------------------
	>>> ### plot config
	>>> ###----------------------------------------
	>>> ax.set_title(label=title, fontsize=20, y=1.5)
	>>> ax.set_xlabel(xlabel="t'", fontsize=15)
	>>> ax.set_ylabel(ylabel="windowsize index", fontsize=15, rotation=0)
	>>> ax.yaxis.set_label_coords(x=0.01, y=1.1) # ylabel position
	>>> ax.tick_params(labelsize=20) # tick fontsize

	>>> fig.savefig(fname=str(plot_images_Path / filename))
	>>> plt.show()

	>>> figsize = (25, 10)
	>>> cmap = "seismic"

	>>> #--------------------------------------------------------------------------------
	>>> # Setting Parameter
	>>> #--------------------------------------------------------------------------------
	>>> title = "{}__channel{}__convolveWindows__windowsize_{}".format(ipynb_title, ch, windowsize)
	>>> filename = title + ".png"

	>>> #----------------------------------------
	>>> # Convolved window size
	>>> #----------------------------------------
	>>> outputs_tmp = hidden_layer_output[:, :, ch].squeeze()
	>>> outputs_tmp = outputs_tmp.T

	>>> # Prepare for convolved
	>>> outputs = np.empty(shape=(0, wave_size - predictsize))
	>>> for window_idx in range(windowsize):
	_shape = outputs_tmp.shape[1]
	# append last
	if window_idx < windowsize-1:
	_val = outputs_tmp[-1, -windowsize+window_idx+1:]
	insert_arr = np.append(arr=outputs_tmp[window_idx],
	values=_val,
	axis=None)
	else:
	insert_arr = outputs_tmp[window_idx]

	# insert first
	_val = outputs_tmp[0, :window_idx]
	insert_arr = np.insert(arr=insert_arr,
	obj=[0 for i in range(window_idx)],
	values=_val,
	).reshape(1, -1)
	# append to the array
	#print(outputs.shape)
	#print(insert_arr.shape)
	outputs = np.append(
	arr=outputs,
	values=insert_arr,
	axis=0,
	)
	>>> print("outputs.shape : ", outputs.shape)
	outputs.shape : (100, 299)

	>>> # Convolved
	>>> outputs_convolve_windows = outputs.sum(axis=0).reshape(1, -1)
	>>> print("outputs_convolve_windows.shape : ", outputs_convolve_windows.shape)
	outputs_convolve_windows.shape : (1, 299)

	def removeIntermidiateChannels(input_array, model, layer_index=0, channel_index=[0]):
	"""
	model : keras model
	layer_index : int
	層の順番
	channel_index=[]
	削除するチャネル
	reference:
	- https://keras.io/getting-started/faq/#how-can-i-obtain-the-output-of-an-intermediate-layer
	"""
	from keras import backend as K

	# check input
	assert type(model) == keras.models.Sequential
	assert type(layer_index) == int
	assert type(channel_index) == list

	# get first half layers output
	get_first_half = K.function(inputs=[model.input],
	outputs=[model.layers[layer_index].output])
	first_half_output = get_first_half(inputs=[input_array])[0]

	# remove channels
	shape = first_half_output.shape[:2]
	for idx in channel_index:
	first_half_output[:,:,idx] = np.zeros(shape)

	# get second half layers output
	get_second_half = K.function(inputs=[model.layers[layer_index+1].input],
	outputs=[model.output])
	second_half_output = get_second_half(inputs=[first_half_output])[0]
	return second_half_output

	>>> channels_num = int(model.layers[0].output.shape[2])

	>>> mse_remove2ch = np.zeros((channels_num, channels_num))
	>>> mse_remove2ch.shape
	(8, 8)

	>>> fig = plt.figure(figsize=(50, 50))
	>>> for ch1 in range(channels_num):
	for ch2 in range(channels_num):
	if ch1 == ch2:
	ax = fig.add_subplot(channels_num, channels_num, ch1*channels_num+ch2+1)
	#ax.plot(t, t)
	else:
	ax = fig.add_subplot(channels_num, channels_num, ch1*channels_num+ch2+1)
	ax.plot(t, wave)
	last_layer_output = removeIntermidiateChannels(input_array=input_arr,
	model=model,
	layer_index=0,
	channel_index=[ch1, ch2])
	ax.plot(t[-len(last_layer_output):], last_layer_output.squeeze())
	mse = mean_squared_error(y_true=wave[windowsize:], y_pred=last_layer_output)
	ax.set_title(label="(ch{}, ch{})'s, MSE : {}".format(ch1, ch2, mse))
	mse_remove2ch[ch1, ch2] = mse
	>>> plt.show()

【深層学習】時系列データに対する１次元畳み込み層の出力を可視化

本記事の目的

目次

環境

ソースコード

サンプル時系列データの作成

一次元畳み込み層による時系列予測モデル作成

入力データの前処理

予測モデル作成 (Keras)

モデルの学習

学習過程の確認

中間層Conv1Dの出力を取得と可視化

学習済みモデルの読み込み

入力データの作成と処理

中間層の出力の取得方法

conv1d_1(Conv1D)の出力の描画

チャネル1の描画

(batch, steps) で描画

steps分を足しあわせて描画

すべてのチャネルを入力波形と重ねて描画

各チャネルごとに入力波形と重ねて描画

特定のチャネルを削除した予測モデル

2つのチャネルを削除

正解波形と予測波形の比較

MSE(二乗和誤差)のカラーマップ表示

最後に

参考

その他の記事

関連職種

`conv1d_1(Conv1D)`の出力の描画