Ladder Netwoksによる半教師あり学習
機械学習エンジニアインターン生の杉崎です。今回はLadder Network1という半教師あり学習の手法と実装について書きます。
目次
ソースコード
半教師あり学習とは
深層学習は大きく以下の3種類に分類され、それぞれにメリットデメリットが存在します。
- 教師あり学習
- 入力データ(x)と教師データ(y)からなるデータセットを使ってxからyを推論できるようにモデルを学習する
- メリット : 精度の高いモデルを学習させることができる
- デメリット : 入力データに対して教師データを作成する作業(ラベリングなど)のコストが高い
- 教師なし学習
- 教師データ(y)を必要とせず、入力データの特徴を把握してデータ同士の関係性などからクラスタリング等に用いられる
- メリット : 入力データを集めるだけでよく、教師データを作成するコストが無い
- デメリット : 教師あり学習に比べて分類精度等が劣る
- 半教師あり学習
- 少量のラベル付きデータ(入力データ(x)と教師データ(y)の対からなるデータセット)と大量のラベル無しデータ(入力データ(x)のみ)を持つとき、ラベル無しデータを用いることでラベル付きデータのみに教師あり学習を適用したときよりも高い精度や汎化性能を持つモデルを学習させる
- メリット : 大量の入力データに対して教師データを作成するコストを抑えることができる。
- デメリット : ラベル付きデータに偏りがあると上手くモデルが学習できなくなる
以上からわかるように半教師あり学習は教師ありと教師なしの中間にあたるものになります。
ラベル無しデータが重要な役割を果たす例としては以下のスライド2の4〜9ページやこちらのサイトにうまく図にまとまっています。
半教ラベル無しデータを含む問題を解くうえで単純な方法は潜在変数モデル(潜在空間モデル)を利用することです。3
最初に入力データを推論しやすい形のデータに変換する手法です。ここでは変換後のデータを潜在変数、その座標空間を潜在空間とよぶことにします。オートエンコーダ(以下スライド5)などを用いた半教師あり学習は良い潜在変数を得るために層を学習します。しかし、単層(オートエンコーダ)では表現力が足りず精度が上がらないため、層を深くする研究が行われていました。
次で紹介するLadder Networksという手法は、デノイジングオートエンコーダ(denoising autoencoder, dAE)やデノイジングソース分割(denoising source separation, DSS)などの手法を深層学習に応用したものになります。
Ladder Networks
2015年に提案4されたLadder Networksという手法を半教師あり学習に応用した内容の論文1があり、今回はこの内容に沿っていきます。
基本的な考え方
Ladder Networksの潜在変数モデルであり、デノイジングオートエンコーダ(denoising autoencoder, dAE)やデノイジングソース分割(denoising source separation, DSS)などのノイズ除去という概念が基礎にあります。
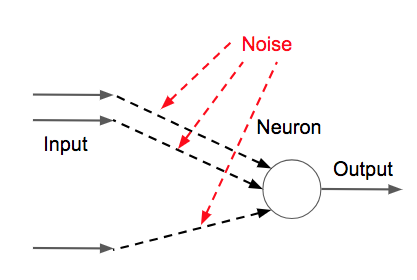
ノイズ除去(denoising)とは入力データ(\(x\))にあえてノイズを加え(\(\tilde{x}\))、
$$ \tilde{x} = x + noise $$
元の入力データ(\(x\))を復元することです。その処理を行う関数\( g(\cdot) \)をdenoising functionと言います。
$$ x \approx \hat{x} = g( \tilde{x} ) $$
この関数をコスト関数\(||\hat{x}-x||^2\)の最小化で求めることになります。
入力データを入力層の出力とみなして\(x=z^{(0)}\)、denoising後のデータ(reconstruction)を\( \hat{z}^{(0)} = g(\tilde{z}^{(0)}) \)と表すことで以下のような図であることがわかります。
dAEの場合は、観測値(\(l=0\))のみを使って学習するのに対して、DSSでは潜在変数である\(l=1\)層目の、ノイズ無し出力を\( z^{(1)} \)とおいて
$$ z^{(1)} = f^{(1)}( z^{(0)} ) $$
となる一層目の関数\(f(\cdot)\)で与えます。そして、denoising関数\(g(\cdot)\)を用いて
$$ z^{(1)} \approx \hat{z}^{(1)} = g^{(1)} ( \tilde{z}^{(1)} ) $$
となるものをコスト\(C_d^{(1)} = || \hat{z}^{(1)} – z^{(1)} ||^2 \)の最小化によって求めます。
このとき、\(z\)を標準化することでdenoising関数\(g(\cdot) = 1\)となることを防いでいます。
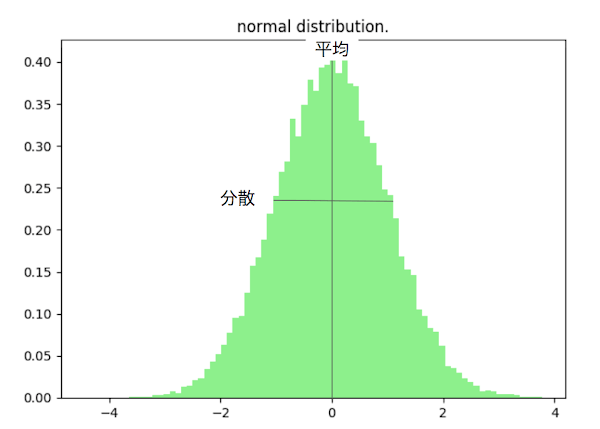
下図1は2つの山の確率分布を持つ\(z\)がCleanで、それにノイズをくわえた\(\tilde{z}\)がCorruptedにあたります。また、紫の線はdenoising関数\(g(\cdot)\)です。
すると、それぞれの確率密度関数(右と上)を比較することにより、山がCleanよりCorruptedのほうが横に広がっているがわかります。これがノイズの影響です。しかし、一方で、denoising関数はこのノイズの影響をなくすように働いていることがわかります。これが
$$ z^{(l)} \approx \hat{z}^{(l)} = g( \tilde{z}^{(l)} ) $$
を表しています。
さて、Ladder Networksとは、このDSSの層を深くしたもの2_9であり、各層の計算は今まで見てきた以下の3式を用います。
$$ z^{(l)} = f^{(l)}( z^{(l-1)} ) $$
$$ z^{(l)} \approx \hat{z}^{(l)} = g( \tilde{z}^{(l)} ) $$
$$ C_d^{(l)} = || \hat{z}^{(l)} – z^{(l)} ||^2 $$
これを2層のネットワークとして図に表したのが以下の図,sup>[1],/sup>になります。(\(x\)はすべて\(l=0\)の\(z^{(l)}\)と読み替えてください。)
後の節で詳しく見ていきたいと思います。
成り立ち
Ladder Networksの成り立ちは以下のスライド24〜29にわかりやすく図になっています。言葉で表現すると、
1. [スライド24] 普通のNeurul Netではラベル無しデータを使えず、学習データに過適合し、過学習してしまう
2. [スライド24] 入力データにノイズを加えることで分離平面をそれぞれのデータ分布から遠くにとることができるようになる
3. [スライド25] 今までは教師ありデータによるSupervised Lossを計算していたが、Decoderを加えることで教師なしデータを含めたすべての入力データに対してReconstruction Lossを計算でき、ラベル無しデータも学習に取り入れることが可能になった
4. [スライド26] Decoderにノイズ入り入力データの情報も組み合わせることで入力分布情報を利用したdenoisingが可能になった
5. [スライド27] 層を深くし、各中間層に対するフィードバックを利用する
6. [スライド28] 入力だけでなく中間層に対してもノイズを混ぜることで、更にロバストなモデルになる
7. [スライド29] Ladder Networks : 深くした各層のDecode出力に対してReconstruction Lossを計算する
アルゴリズム
論文1に掲載されているアルゴリズムは以下のようになっておりますが、今回用意したTensorFlowのコードに合わせて5層のMLP(多層パーセプトロン)の場合に限って図解したいと思います。
ただし、\(\lambda_l\)はハイパーパラメータ、\(m_l\)は\(l\)層目の幅で、\(\boldsymbol{W}^{(l)}, \boldsymbol{\gamma}^{(l)}, \boldsymbol{\beta}^{(l)}, \boldsymbol{V}^{(l)}, \boldsymbol{a}_i^{(l)} \)がモデルのパラメータになります。
モデルは上図におけるCorrupted Encoder, Decoder, Clean Encoderの3種類の多層レイヤから成ります。Forwardの計算式は図に書いてあるとおりです。式中の\(ACT\),\(B_N\)はそれぞれ活性化関数、バッチ標準化処理を表しています。コード中ではrelu関数を活性化関数として用いています。
Decoder内のカラー付きの変数は青と赤の矢印が示す通り両隣のEncoderから導出したものです。
モデルの学習中のパラメータ更新のためのコスト関数(損失関数)は以下のように定義されています。(Pはラベルの確率を返し、コードではsoftmax関数を使用しています。)
$$ C_c = – \frac{1}{N} \sum_{n=1}^{N} \log P \left( \boldsymbol{\tilde{y}} = t(n) | \boldsymbol{x}(n) \right) $$
$$ C_d = \sum_{l=0}^{L} \lambda_l C_d^{(l)} = \sum_{l=0}^{L} \frac{\lambda_l}{N \cdot m_l} \sum_{n=1}^{N} || \boldsymbol{z}^{(l)}(n) – \boldsymbol{\hat{z}}_{BN}^{(l)}(n) ||^2 $$
$$ C = C_c + C_d $$
\(C_c\)の箇所はCorrupted Encoderの出力のコスト関数で正解ラベル\(t(n)\)を用いていることからわかるようにこれらはラベル有りデータが入力されたときにのみ計算されます。
\(C_d\)はDecoderのコスト関数 (Reconstruction Loss) であり、各レイヤごとにClean Encoderの各層の出力と比較しています。
つまり、\(C_c\)を教師あり学習から求まるコスト関数とし、\(C_d\)が教師なし学習から求まるコスト関数になります。
ここで一つ注意が必要なのはコスト関数に組み込まれるのはCorrupted Encoderの出力ですが、実際に予測を行う際はClean Encoderの出力\(y\)が予測結果になることです。
ソースコード中におけるEncoder, Decoder はそれぞれ以下の部分に記述されています。EncoderがCorruptedかCleanの差は引数で与えているnoise_stdが0か否かで決まります。
def encoder(inputs, noise_std):
"""
Parameters
----------
inputs :
noised_std : float,
noised_std != 0.0 --> Corrupted Encoder
noised_std == 0.0 --> Clean Encoder
Globals
-------
split_lu : func
layer_sizes : list
weights : dict
join : func
batch_normalization : func
running_mean, running_var : list, These list stores average mean and variance of all layers
Returns
-------
"""
h = inputs + tf.random_normal(tf.shape(inputs)) * noise_std # add noise to input
d = {} # to store the pre-activation, activation, mean and variance for each layer
# The data for labeled and unlabeled examples are stored separately
d['labeled'] = {'z': {}, 'm': {}, 'v': {}, 'h': {}} # m=mean, v=variance
d['unlabeled'] = {'z': {}, 'm': {}, 'v': {}, 'h': {}} # m=mean, v=variance
d['labeled']['z'][0], d['unlabeled']['z'][0] = split_lu(h)
for l in range(1, L+1):
print( "Layer {:>3}: {:>5} -> {:>5}".format(l,layer_sizes[l-1], layer_sizes[l]) )
d['labeled']['h'][l-1], d['unlabeled']['h'][l-1] = split_lu(h)
z_pre = tf.matmul(h, weights['W'][l-1]) # pre-activation
z_pre_l, z_pre_u = split_lu(z_pre) # split labeled and unlabeled examples
m, v = tf.nn.moments(z_pre_u, axes=[0]) # compute mean, variance using twice later (efficiency)
#----------------------------------------
# if training:
def training_batch_norm():
# Training batch normalization
# batch normalization for labeled and unlabeled examples is performed separately
if noise_std > 0: # Corrupted Encoder
# Corrupted encoder
# batch normalization + noise
z = join(batch_normalization(z_pre_l), batch_normalization(z_pre_u, m, v))
z += tf.random_normal(tf.shape(z_pre)) * noise_std
else: # Clean Encoder
# Clean encoder
# batch normalization + update the average mean and variance using batch mean and variance of labeled examples
z = join(update_batch_normalization(z_pre_l, l), batch_normalization(z_pre_u, m, v))
return z
# else:
def eval_batch_norm():
# Evaluation batch normalization
# obtain average mean and variance and use it to normalize the batch
mean, var = ewma.average(running_mean[l-1]), ewma.average(running_var[l-1])
z = batch_normalization(z_pre, mean, var)
# Instead of the above statement, the use of the following 2 statements containing a typo
# consistently produces a 0.2% higher accuracy for unclear reasons.
# m_l, v_l = tf.nn.moments(z_pre_l, axes=[0])
# z = join(batch_normalization(z_pre_l, m_l, mean, var), batch_normalization(z_pre_u, mean, var))
return z
# perform batch normalization according to value of boolean "training" placeholder:
z = tf.cond(pred=training, true_fn=training_batch_norm, false_fn=eval_batch_norm)
#----------------------------------------
if l == L:
# use softmax activation in output layer
h = tf.nn.softmax(weights['gamma'][l-1] * (z + weights["beta"][l-1]))
else:
# use ReLU activation in hidden layers
h = tf.nn.relu(z + weights["beta"][l-1])
d['labeled']['z'][l] , d['unlabeled']['z'][l] = split_lu(z)
d['unlabeled']['m'][l], d['unlabeled']['v'][l] = m, v # save mean and variance of unlabeled examples for decoding
d['labeled']['h'][l], d['unlabeled']['h'][l] = split_lu(h)
return h, d
# Decoder
def g_gauss(z_c, u, size):
"""
gaussian denoising function proposed in the original paper
Parameters
----------
z_c : z in Corrupted Layer
u : batch normalized h~(l) (l=0,...,L)
size :
Returns
-------
"""
w_i = lambda inits, name: tf.Variable(inits * tf.ones([size]), name=name)
a1 = w_i(0., 'a1')
a2 = w_i(1., 'a2')
a3 = w_i(0., 'a3')
a4 = w_i(0., 'a4')
a5 = w_i(0., 'a5')
a6 = w_i(0., 'a6')
a7 = w_i(1., 'a7')
a8 = w_i(0., 'a8')
a9 = w_i(0., 'a9')
a10 = w_i(0., 'a10')
mu = a1 * tf.sigmoid(a2 * u + a3) + a4 * u + a5
v = a6 * tf.sigmoid(a7 * u + a8) + a9 * u + a10
z_est = (z_c - mu) * v + mu
return z_est
print( "=== Decoder ===" )
with tf.name_scope(name="Decoder"):
z_est = {}
d_cost = [] # to store the denoising cost of all layers
for l in range(L, -1, -1):
print( "Layer {:>2}: {:>5} -> {:>5}, denoising cost: {:>7.1f}".format(l, layer_sizes[l+1] if l+1 , len(layer_sizes) else "None", layer_sizes[l], denoising_cost[l]))
z, z_c = clean['unlabeled']['z'][l], corr['unlabeled']['z'][l]
m, v = clean['unlabeled']['m'].get(l, 0), clean['unlabeled']['v'].get(l, 1-1e-10)
if l == L:
u = unlabeled(y_c)
else:
u = tf.matmul(z_est[l+1], weights['V'][l])
u = batch_normalization(u)
z_est[l] = g_gauss(z_c, u, layer_sizes[l])
z_est_bn = (z_est[l] - m) / v
# append the cost of this layer to d_cost
d_cost.append((tf.reduce_mean(tf.reduce_sum(tf.square(z_est_bn - z), 1)) / layer_sizes[l]) * denoising_cost[l])
精度比較
今回比較するのは以下の3つのコードです。
全データ6万のMNISTトレーニングデータに対して
1. ラベル有りが100枚、その他はラベル無しをLadder Networksで実装
2. ラベル有りが100枚、その他はラベル無しを単純なMLPで実装
3. 全データラベル有りを単純なMLPで実装
各コードはGitHub上に載せてあります。
最終的な分類精度は以下のようになりました。
| 手法 | テスト精度 |
|---|---|
| 1 | 98.79 % |
| 2 | 70.17 % |
| 3 | 98.01 % |
これより、通常のMLPであれば過学習してしまい精度が上がらないところ、Ladder Networksを用いることですべてのデータを使ったときのMLPの精度と同じくらいの精度が出ていることがわかります。
この他に成り立ちで紹介したスライドには精度の比較が載っており、大変参考になります。
感想
今回は半教師あり学習手法としてのLadder Networksについて書きました。元の論文1の内容は比較的わかりやすく書かれているので読んで見ることをおすすめします。本記事がその一助になれば幸いです。
参考
その他の記事
Other Articles


関連職種
Recruit