WebGLでレイマーチングを使ったCSGを実現する

Tweet

TL;DR これ作った。

こんにちは。カブクでThree.js周りを担当していたけど、現状ほとんど触れていないあんどうです。

今はもうただひたすらに、目標をセンターに入れて座標変換、目標をセンターに入れて座標変換・・・。もちろんそれはそれで面白みもありますが、たまにはもうちょっとキラキラしたこともやりたい！輝きたい！ということで、今回開発者ブログの場を借りて輝こうと思います。

CSG

現在、弊社の開発しているサービスの主なターゲットは製造業です。個人的にはもう少し付加製造（3Dプリンタ）が流行ると嬉しいのですが、現実問題として世の中のほとんどのものは切削加工で製造されています。成形加工もありますが、そこで使用される型はほとんどが切削加工品でしょう。私が3Dモデル生成している製品もご多分に漏れず切削加工で製造されます。最終的にはこのモデルをブラウザ上で3Dプレビュー表示したいのですが、こういった切削で製造される製品の3Dモデルはどういう形式で表現するのが適切なのでしょう？

ここで、切削は「土台となる形状から不要な形状を除く」という加工です。つまり

最終形状 = 土台形状 - 不要形状

と表すことができます。実はこのような関係をそのままの形で表現できるモデリング技法があるのです。それがCSG（Constructive Solid Geometry）です。

https://ja.wikipedia.org/wiki/Constructive_Solid_Geometry

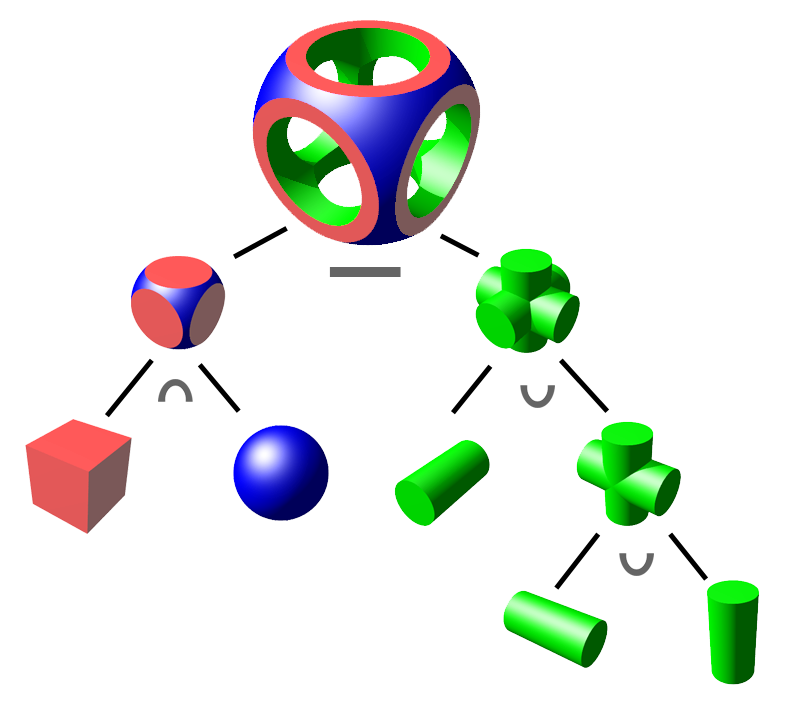
CSGでは直方体や円柱、球などの基本形状と、それらに対するブーリアン演算（和・差・交差）の組み合わせで形状を表現します。このCSGであれば切削加工で製造される形状を自然に表現できそうです。ただ、ひとつ問題があります。任意のポリゴンモデルに対するCSGは非常に重たい処理なのです。なぜそうなるかは実際の処理を想像してみるとわかるでしょう。ナイーブな実装では、モデルごとに全ポリゴン同士の交差を計算し、交差する場合は交線でポリゴンを分割してモデルを再構築することを、一回のブーリアン演算ごとに行います。交差計算の頻度はBSPなどを使用して減らすこともできますが、それでもブラウザ上でJavaScriptを使用して実行するとなるとなかなかの重さです。下記のサイトでCSGを実際に実行できるので、試してみるといいでしょう。（と書きましたが試してみると意外とサクサクでした。たぶん頂点数が増えると急激に重くなるはず）

https://evanw.github.io/csg.js/

ではCSGは今回のプレビューには使用できないのでしょうか？実はそういうわけでもありません。確かに実際に製造するのであればどこかで上記のような負荷の高い計算が必要になります。しかし、そのような計算はサーバー上で行えばよく、ブラウザ上で行う必要はありません。ブラウザ上で実行したいのはあくまでプレビュー表示であって、実際のポリゴン操作ではないのです。

レイマーチング

レイマーチングはレイトレーシングの一種で、形状をポリゴンではなく距離関数（数式）で定義します。ポリゴンモデルのブーリアン演算は先ほど説明したとおり面倒な処理でしたが、距離関数のブーリアン演算はどうでしょう？

それが実は、ものすごく簡単なのです。

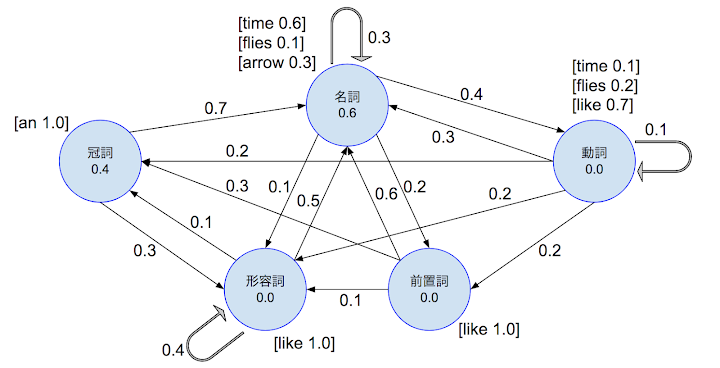
距離関数はある座標からその形状表面への最短距離を返す関数で、返り値はひとつの数値です。例えば形状1の距離関数の値がdist1、形状2の距離関数の値がdist2だとすると、形状1と形状2のブーリアン演算の結果は次のように表せます。

• 和: min(dist1, dist2)
• 差: max(dist1, -dist2)
• 交差: max(dist1, dist2)

ブーリアン演算の説明は後述しますが、レイマーチングではCSGを非常に簡単に実現できることがわかるでしょう。

それではレイマーチングの説明に移ります。先ほども書きましたがレイマーチングでは形状を、与えられた座標からその形状までの最短距離を返す距離関数で表現します。例えば原点にある半径rの球の距離関数は次のようになります。

float sphereDist(vec3 p, float r) {
  return length(p) - r;
}

点pから原点にある半径rの球までの最短距離は、点pから原点までの距離から半径rを引いた値です。なぜそのような式になるかは下の図を見ると明らかでしょう。

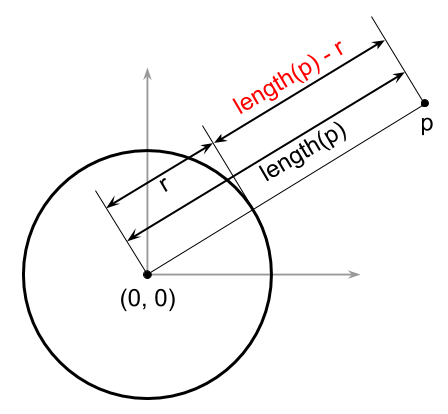
直方体や円柱などの形状も同様に与えられた座標からの最短距離を単純な関数で取得できます。

それでは、それらの距離関数を使用してシーンを描画するにはどうすればいいのでしょう？

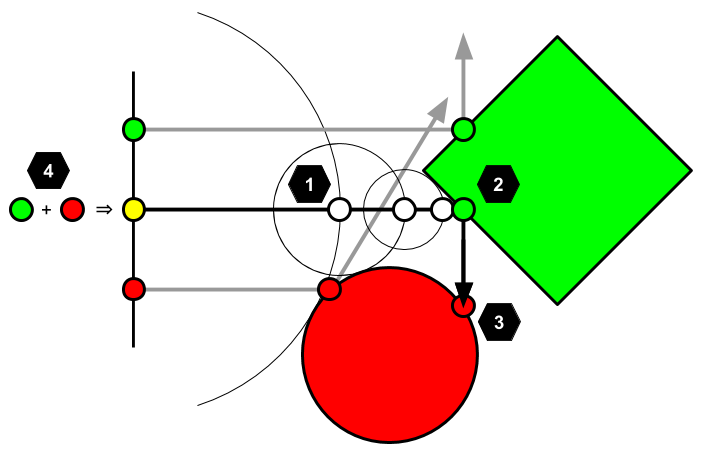
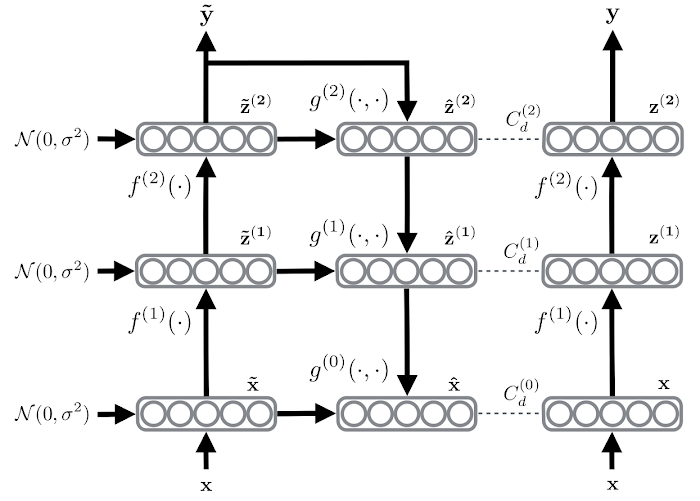
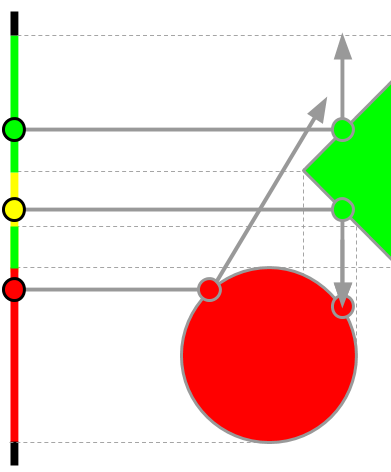
上の図を見てください。レイマーチングはフラグメントシェーダーで実装します。フラグメントシェーダーは簡単に言うと、ピクセルごとに実行されて、そのピクセルの色を決定する小さなプログラムです。左側の垂線がシーンを表示する画面（視錐台の近平面）、その上の緑・黄色・赤の円がスクリーン上の各ピクセル（フラグメント）、そしてその各ピクセルから右に伸びる線がスクリーンから視線方向に伸びるレイ（半直線）だと考えてください。レイがなにかに衝突すると、その衝突した位置の色がフラグメントに設定されます。レイマーチングでフラグメントの色を求める手順は次のとおりです。

1. フラグメントの現在の色を黒（背景色、物体なし）に設定する
2. シーンに存在するすべての物体と現在のレイの先端との距離（距離関数の値）を求める
3. 最も小さい（近い）距離関数の値を選択する
4. 最も小さい距離関数の値が大きければ、レイを進行方向にその距離だけ進め、2に戻る
5. 最も小さい距離関数の値が十分に小さければ、その位置の色を現在の色に加える
   1. 反射を処理する場合は、レイの位置は変更せず、レイの進行方向を衝突位置の法線を使用して反射して、2に戻る
   2. 反射を処理しない場合は、終了する

真ん中の黄色いフラグメントを例にしてレイマーチングの処理を具体的に説明しましょう。まずは左側の黄色い円の位置にレイの先端があるものとします。レイの先端から緑の四角と赤の丸までの最短距離をそれぞれ求めると赤い丸との距離のほうが小さく、しかし十分に小さいわけではないので、得られた距離だけレイを進めます。するとレイの先端が最も左側の白丸の位置に移動します（1）。

同様に緑四角と赤丸との距離を求めると今度も赤丸との距離のほうが小さく、しかし十分に小さいわけではないので、真ん中の白い円の位置までレイを進めます。同様に距離関数の値を求めると今度は緑四角との距離が近いので、右の白い円の位置までレイを進めます。同様に繰り返すと緑の円の位置までレイの先端が進みます（2）。

レイが衝突した点の色が緑なのでフラグメントの色を仮に緑とします。今回は緑四角も赤丸も光を鏡面反射するので、衝突位置の法線を中心として対照になるようにレイの進行方向を変更します。そしてこれまでと同様にレイを進めます。はじめはレイの先端と緑四角が近いためゆっくりと最初の衝突点を離れますが、次第に一回の移動量が大きくなります。そして赤丸との衝突点が近づくに連れて移動量が再び小さくなり、いずれ赤丸に衝突します（3）。

赤丸に衝突したということは、緑四角の衝突点には赤丸の鏡像が写っていることになるので、視点から直接見える緑と、その緑に写っている赤を合成して、フラグメントの色を黄色に設定します（4）。

同様の処理をすべてのフラグメントに対して行うと、次の図の左端の垂線のような（1次元の）シーンが描画されます。

同様な処理を次元をひとつ増やして行えば、3次元空間を平面上に射影できます。

実装

全体的な処理の流れの説明は以上です。ここからはソースコードの説明に移りましょう。レイマーチングの主要なコードについてはThree.jsに付属している例をほぼそのまま使用しています。この例の作者であるgamさんによる説明がQiitaにありますので、そちらも参考にしてください。

https://threejs.org/examples/?q=ray#webgl_raymarching_reflect

なお、今回説明するのは実際にレイマーチングを行っているフラグメントシェーダーのコードだけです。それ以外の部分についてはここでは特に説明しません。興味のある方はソースコードを自分で読んでみてください。Three.jsを使用しているので、それなりに雰囲気で理解できるのではないかと思います。

それでははじめに処理全体を駆動する部分を見ていきます。

void main(void) {
  // レイは画面内でのフラグメントの位置からカメラの向いている方向に飛ばす
  vec2 screenPos = (gl_FragCoord.xy * 2.0 - resolution) / resolution;
  vec4 ndcRay = vec4(screenPos.xy, 1.0, 1.0);
  vec3 rayDirection = (cameraWorldMatrix * cameraProjectionMatrixInverse * ndcRay).xyz;
  rayDirection = normalize(rayDirection);

  // レイの始点はカメラ位置
  vec3 rayOrigin = cameraPosition;

  // フラグメントの初期色を黒に設定
  vec3 color = vec3(0.0);

  vec3 nextRayPos, normal;
  bool hit;
  float attenuation = 1.0;

  // 反射は2回まで処理
  for (int i = 0; i < 3; i++) {
    // レイを飛ばして衝突した位置の色を加算
    color += attenuation * getRayColor(rayOrigin, rayDirection, nextRayPos, normal, hit);

    if (!hit) {
      // レイが物体表面と衝突していなければ反射せずにループを抜ける
      break;
    }

    // レイが物体表面と衝突していれば反射して処理を繰り返す
    
    // 反射するたびに次の色の影響を弱める
    attenuation *= 0.3;

    // 衝突点の法線を使用してレイを反射
    rayDirection = normalize(reflect(rayDirection, normal));

    // 同じ位置で衝突を繰り返さないようにレイの始点をずらす
    rayOrigin = nextRayPos + normal * OFFSET;

  }
  gl_FragColor = vec4(color, 1.0);
}

コメントを多めに入れたのでなんとなく読めるのではないでしょうか。レイマーチングによるレイの衝突確認はforループ内のgetRayColor関数で行います。レイが物体表面に衝突していた場合は同じ処理を繰り返して2回まで反射を処理します。

getRayColor関数のコードは次のとおりです。

vec3 getRayColor(vec3 rayOrigin, vec3 rayDirection, out vec3 rayPosition, out vec3 normal, out bool hit) {
  float dist;
  float depth = 0.0;
  rayPosition = rayOrigin;

  // 距離関数の値だけレイを進める処理を64回繰り返す
  for (int i = 0; i < 64; i++) {
    // 距離関数を実行
    dist = sceneDist(rayPosition);

    // 距離関数の値が十分に小さければ探索を停止
    if (abs(dist) < EPS) {
      hit = true;
      break;
    }

    // 距離関数の値がまだ大きければレイを進めてから処理を繰り返す
    depth += dist;
    rayPosition = rayOrigin + depth * rayDirection;
  }

  if (!hit) {
    // 衝突していなければ物体表面の色は黒
    return vec3(0.0);
  }
    
  // 衝突したら反射の処理で使用するための法線を設定しておく
  normal = getNormal(rayPosition);

  // 光の向きと法線の向きから物体表面の色を取得
  vec3 color = getLightColor(light1Dir, rayDirection, rayPosition, normal)
    + getLightColor(light2Dir, rayDirection, rayPosition, normal);

  // 視点から表面までの距離分だけ色を減衰して返す
  return color - pow(clamp(0.05 * depth, 0.0, 0.6), 2.0);
}

forループ内で呼び出しているsceneDist関数が今回の距離関数で、シーン内の最も近い物体からの距離distを返します。distの値が小さければレイの進行を停止して、その位置の色を返します。distの値が大きければレイを進める処理を繰り返し、64回レイを進めても物体との衝突が発生しなければ、黒色を返します。

それでは今回の距離関数sceneDistの実装を見てみましょう。

float sceneDist(vec3 p) {
  float cube = boxDist(p, vec3(2., 2., 2.));
  float cylinder = cylinderDist(p, 0.5, 4.0);
  float sphere = sphereDist(p, 1.);
  return differ(unite(cube, cylinder), sphere);
}

まだ説明していない関数ばかりですが、やりたいことは何となく分かるのではないでしょうか。各辺の長さ2の立方体（cube）と、半径0.5で高さ4の円柱（cylinder）と、半径1の球（sphere）があり、立方体と円柱を結合（unite(cube, cylinder)）した形状から、球の形状を取り除いて（differ(..., sphere)）います。

原点にある球と立方体と円柱の距離関数はそれぞれ次のようになります。

float sphereDist(vec3 p, float r) {
  return length(p) - r;
}

float boxDist(vec3 p, vec3 size) {
  vec3 d = abs(p) - size / 2.0;
  return length(max(d,0.0)) + min(max(d.x,max(d.y,d.z)),0.0);
}

float cylinderDist(vec3 p, float radius, float height) {
  vec2 d = vec2( length(p.xz)-radius, abs(p.y) - height / 2.0);
  return min(max(d.x,d.y),0.0) + length(max(d,0.0));
}

詳細は省略しますが、非常に簡単な式で基本形状を定義できていることがわかります。下のサイトでさまざまな形状の距離関数が紹介されているので興味のある方はぜひ見てみてください。

http://iquilezles.org/www/articles/distfunctions/distfunctions.htm

最後にCSGの実装について説明します。先ほど紹介しましたが、ここでソースコードを再掲しておきます。

float unite(float dist1, float dist2) {
  return min(dist1, dist2);
}

float differ(float dist1, float dist2) {
  return max(dist1, -dist2);
}

float intersect(float dist1, float dist2) {
  return max(dist1, dist2);
}

なぜこれでうまくいくのか、単純すぎて逆にわかりにくいかもしれませんが、図にすると明らかでしょう。

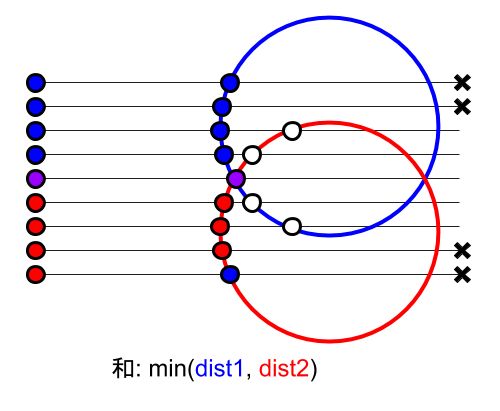
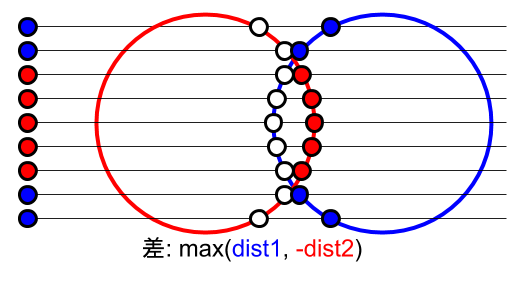
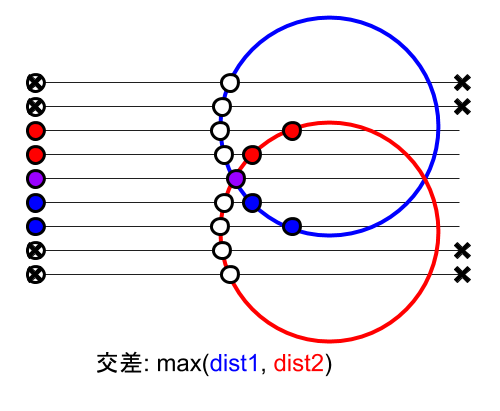
左側に縦一列に並んでいる丸から右方向にレイを飛ばし、各物体（大きな赤丸と青丸）と交わる点までの距離を計算して、maxであれば右側にある方、minであれば左側にある方を採用します。なお、距離を負数にすると画面から見て裏面が使用されます。基本的にはただ距離の大小を比較するだけの非常に単純な処理ですが、それぞれ対象となる点までの距離を正しく返すことができています。

確認

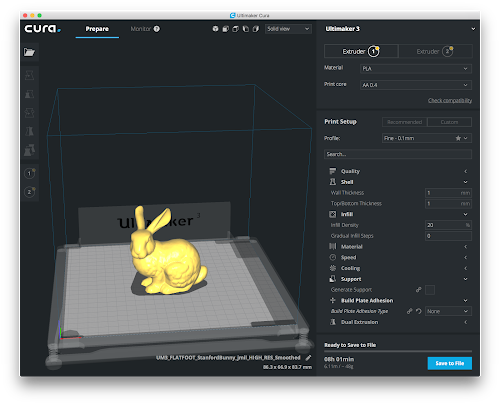
それでは実際に動かしてみましょう。

https://technohippy.github.io/raymarching-csg/

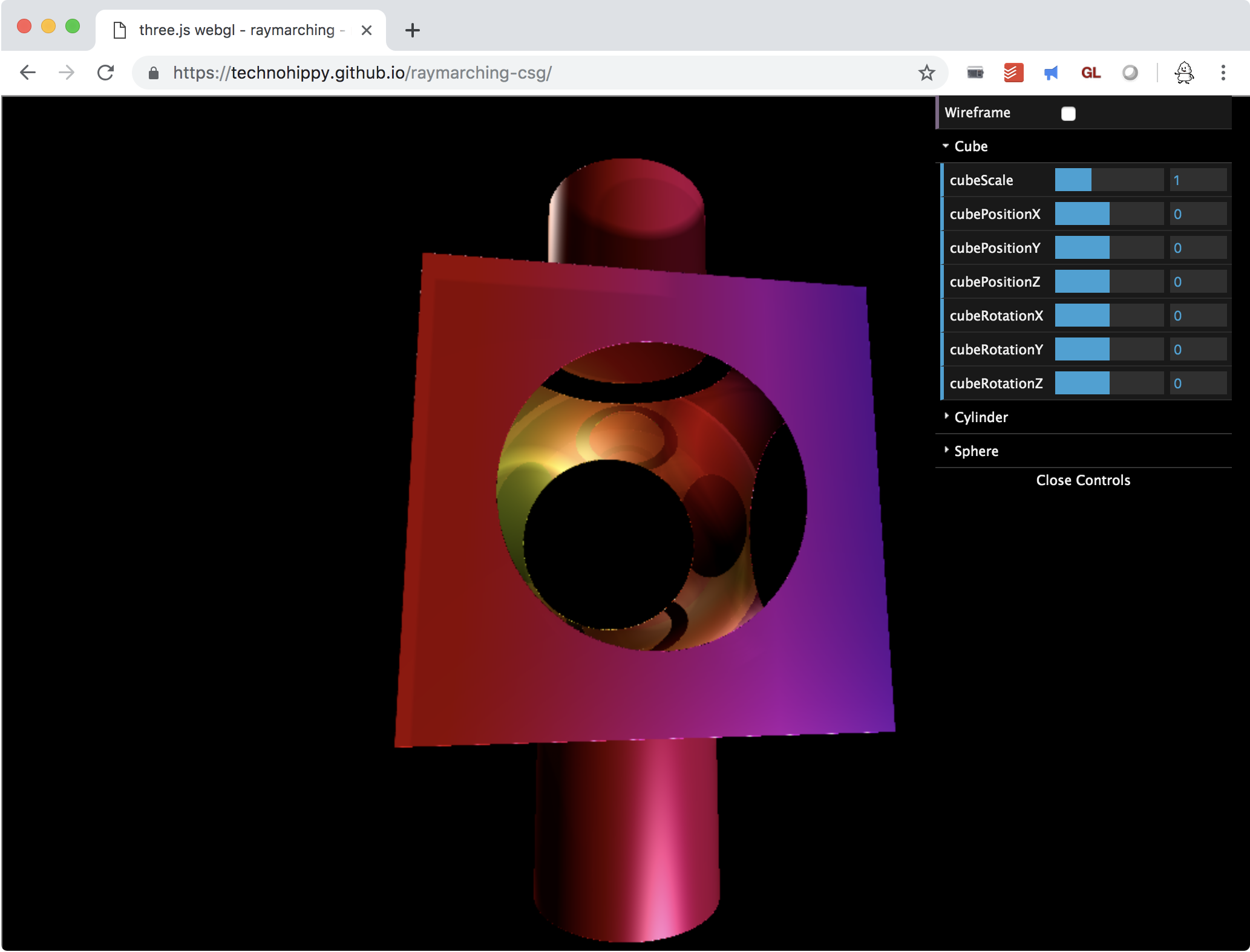
立方体と円柱を結合してから球が取り除かれた期待通りの形状が描画されています。上記サンプルではワイヤーフレームのオーバーレイに加え、各形状の回転や平行移動、拡大縮小も試せるようにしてありますので、ぜひいろいろと触ってみてください。ソースコードも以下で確認できます。

https://github.com/technohippy/raymarching-csg

さいごに

株式会社カブクではキラキラ輝きたいピュアで素敵な開発者を募集しています。